Mengenal Metode Independent Component Analysis (ICA)

Apa itu ICA?

Independent Component Analysis (ICA) adalah metode matematika yang digunakan untuk “memisahkan” campuran sinyal menjadi sinyal-sinyal aslinya, dengan cara menemukan pola-pola unik di dalam campuran tersebut. Bayangkan seperti ini:

1. Misalnya ada pesta: Di dalam sebuah ruangan, ada beberapa orang berbicara bersamaan. Kamu mendengar suara-suara itu bercampur menjadi satu karena kamu hanya punya satu telinga.
2. Campuran suara: Bayangkan mikrofon di tengah ruangan merekam semua suara yang ada. Mikrofon itu menangkap campuran suara semua orang.
3. Tujuan ICA: ICA berusaha untuk “memisahkan” suara orang-orang itu dari campuran tadi sehingga kamu bisa mendengar setiap suara secara terpisah, seperti suara A, B, dan C masing-masing.
4. Bagaimana ICA melakukannya?
   • ICA mencoba mencari pola-pola yang unik dari setiap suara. Misalnya, suara seseorang punya nada atau volume tertentu yang berbeda dari orang lain.
   • Dengan menggunakan pola-pola ini, ICA memisahkan campuran menjadi bagian-bagian yang terpisah (sinyal aslinya).
5. Contoh nyata:
   • Di dunia nyata, ini bisa dipakai untuk memisahkan suara seseorang dari musik latar belakang (seperti fitur noise cancellation pada headphone).
   • Dalam penelitian, ICA sering digunakan untuk memisahkan sinyal otak (EEG) dari “noise” seperti gerakan mata atau kedipan.

Implementasi Python

Berikut adalah contoh program Python sederhana yang menggunakan pustaka Scikit-learn untuk melakukan Independent Component Analysis (ICA). Program ini akan memisahkan sinyal campuran menjadi sinyal aslinya.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA

# 1. Membuat sinyal sumber (misalnya dua sinyal asli)
np.random.seed(0)
time = np.linspace(0, 10, 1000)

# Sinyal asli: gelombang sinus dan gelombang persegi
s1 = np.sin(2 * time)  # Sinyal sinus
s2 = np.sign(np.sin(3 * time))  # Sinyal persegi

# Gabungkan sinyal asli menjadi array
S = np.c_[s1, s2]

# 2. Membuat campuran sinyal (seperti mikrofon merekam campuran)
A = np.array([[1, 0.5], [0.5, 1]])  # Matriks pencampuran
X = S.dot(A.T)  # Campuran sinyal

# 3. Terapkan ICA untuk memisahkan sinyal
ica = FastICA(n_components=2, random_state=0)
S_reconstructed = ica.fit_transform(X)  # Memisahkan sinyal

# 4. Plot sinyal asli, campuran, dan hasil rekonstruksi
plt.figure(figsize=(10, 6))

# Sinyal asli
plt.subplot(3, 1, 1)
plt.title("Sinyal Asli")
plt.plot(time, s1, label="Sinyal 1")
plt.plot(time, s2, label="Sinyal 2")
plt.legend()

# Sinyal campuran
plt.subplot(3, 1, 2)
plt.title("Sinyal Campuran")
plt.plot(time, X[:, 0], label="Campuran 1")
plt.plot(time, X[:, 1], label="Campuran 2")
plt.legend()

# Sinyal hasil ICA
plt.subplot(3, 1, 3)
plt.title("Sinyal Rekonstruksi (ICA)")
plt.plot(time, S_reconstructed[:, 0], label="Rekonstruksi 1")
plt.plot(time, S_reconstructed[:, 1], label="Rekonstruksi 2")
plt.legend()

plt.tight_layout()
plt.show()

Penjelasan Program

1. Sinyal asli:
   • s1 adalah gelombang sinus.
   • s2 adalah gelombang persegi.
2. Campuran sinyal:
   • Matriks pencampuran A digunakan untuk mencampur dua sinyal menjadi dua sinyal campuran.
3. ICA:
   • Algoritma ICA diterapkan menggunakan pustaka FastICA dari Scikit-learn untuk memisahkan sinyal campuran menjadi sinyal-sinyal aslinya.
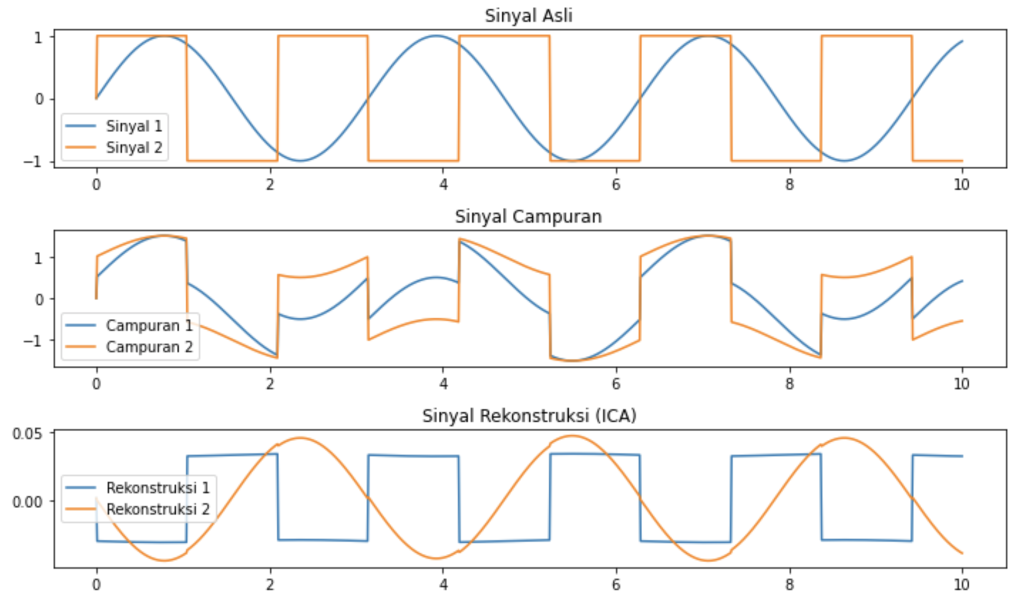
4. Hasil visualisasi:
   • Plot pertama menunjukkan sinyal asli.
   • Plot kedua menunjukkan sinyal yang bercampur.
   • Plot ketiga menunjukkan sinyal yang dipisahkan kembali oleh ICA.

Cara Menjalankan

• Pastikan pustaka NumPy, Matplotlib, dan Scikit-learn sudah terinstall. Kamu bisa menginstallnya dengan:bashCopyEditpip install numpy matplotlib scikit-learn

Jika dijalankan, program ini akan memvisualisasikan bagaimana ICA berhasil memisahkan sinyal yang telah tercampur.